Free Rigid Body Collisions
A free rigid body collision is an instance where two non-anchored or movable bodies impact one another, and we are treating at least one of those bodies as a rigid body where rotation can occur.
Rigid Body Inelastic Impacts
We will begin our analysis with inelastic impacts, where the bodies stick together after impact. In these systems we will first recognize that the large internal impulsive forces between the bodies colliding dwarf any external forces at the time of collision. Though the linear momentum of each body individually will change drastically, the linear momentum of the system as a whole will not change. Assuming we call our two bodies A and B and we take the velocities at the center of mass (G), we arrive at the vector equation below.
| \[ m_{A} \vec{v_{GAi}}+m_{B} \vec{v_{GBi}}= (m_{A}+m_{B}) \vec{v_{GABf}}\] |
Furthermore, breaking this vector equation down into x and y components, we will arrive at the following set of scalar equations.
| \[m_{A} v_{GAix}+m_{B} v_{GBix}= (m_{A}+m_{B}) v_{GABfx}\] |
| \[m_{A} v_{GAiy}+m_{B} v_{GBiy}= (m_{A}+m_{B}) v_{GABfy}\] |
In addition to the linear momentum being conserved, the angular momentum is also conserved for the system as a whole, as the large impact's angular impulse is internal. The angular momentum can be taken about any point, so long as we are consistent throughout the equation. For more information on calculating the angular momentum about various points, consult the prior sections.
| \[angular\ momentum\ initial = angular\ momentum\ final\] |
Rigid Body Elastic and Semi-Elastic Impacts
In an elastic or semi-elastic impact the bodies do not stick together after impact and will have separate linear and angular velocities post impact. With potential linear velocities in the x and y directions for each body, as well as separate angular velocities post impact, we will potentially have six unknowns to solve for. This also means that we will need six equations to solve for all of those unknowns.
The first three equations will be the same as with the inelastic impact. Both linear momentum and angular momentum will be conserved for the system as a whole.
| \[m_{A} v_{GAix}+m_{B} v_{GBix}= m_{A} v_{GAfx}+m_{B} v_{GBfx}\] |
| \[m_{A} v_{GAiy}+m_{B} v_{GBiy}= m_{A} v_{GAfy}+m_{B} v_{GBfy}\] |
| \[angular\ momentum\ initial = angular\ momentum\ final\] |
As before, the linear velocities need to be taken at the center of mass (G), and the angular momentum can be taken about any point so long as we are consistent with the point we are taking it about throughout the equation.
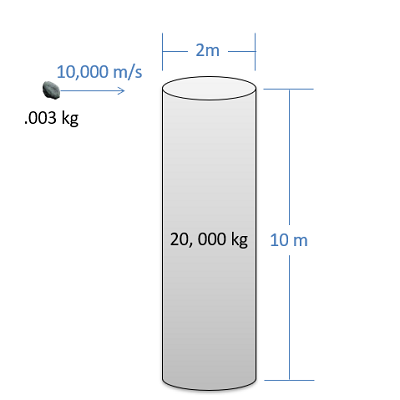
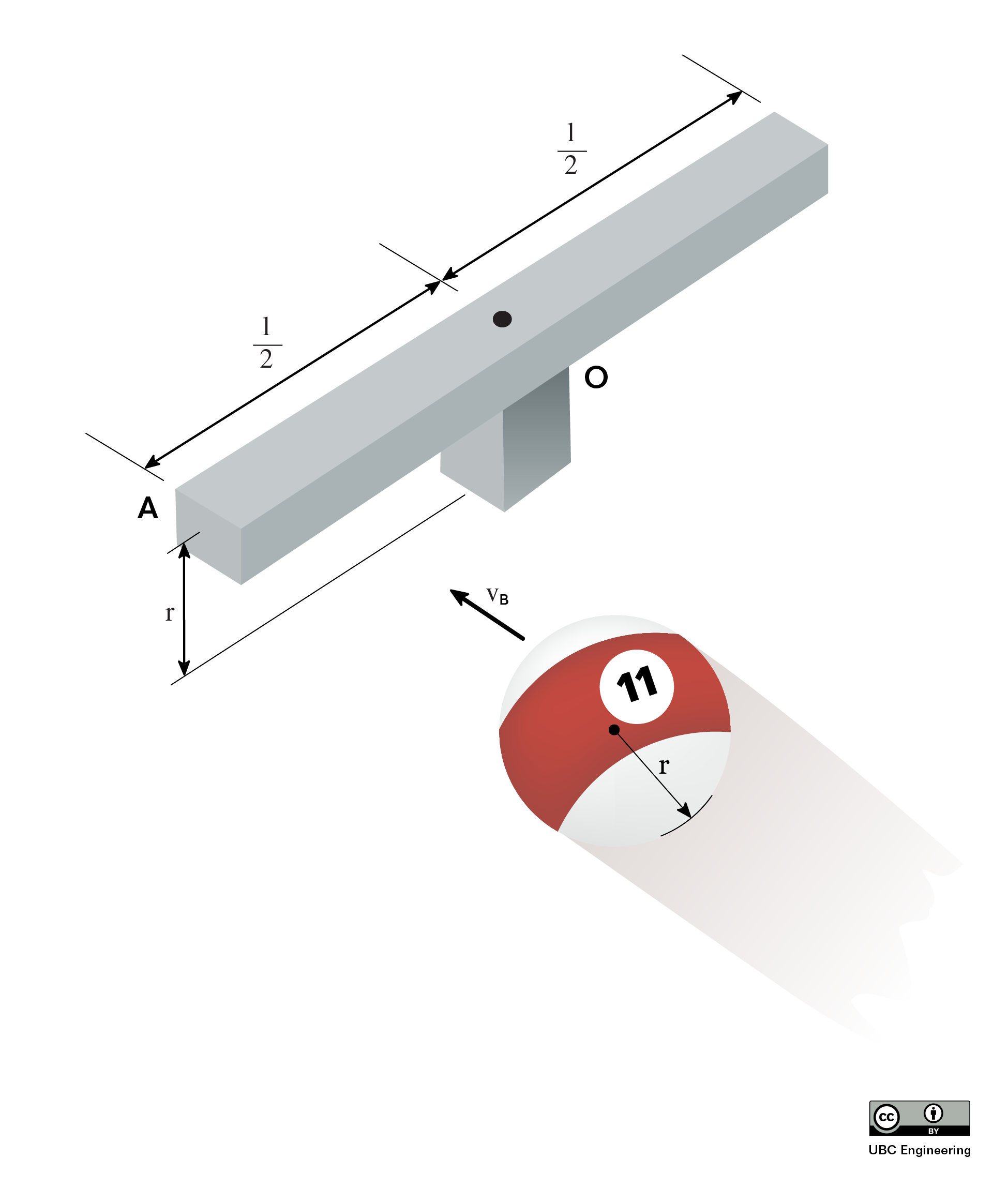
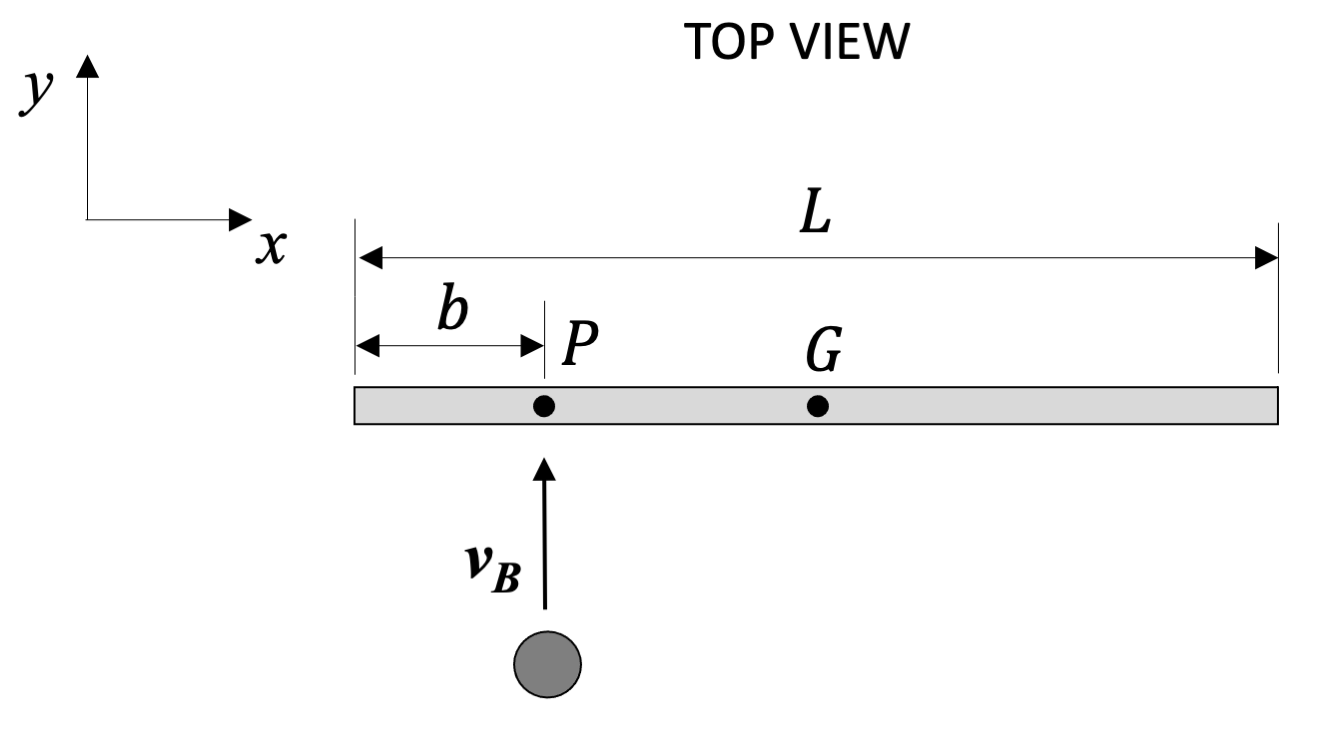
To add to those three equations, as with rigid body surface impacts, we can assume the angular momentum of each body individually is conserved about the point of impact (P). This is because there will be no impulse angular impulse during the collision about this point in particular. As this point is almost always not at the center of mass of either body, we wind up with the following two equations.
| \[ I_{GA} * \vec{\omega_{Ai}} + \left( \vec{r}_{G_A/P} \times m_A \vec{v_{GBi}} \right) = I_{GA} * \vec{\omega_{Af}} + \left( \vec{r}_{G_A/P} \times m_A \vec{v_{GAf}} \right)\] |
| \[ I_{GB} * \vec{\omega_{Bi}} + \left( \vec{r}_{G_B/P} \times m_B \vec{v_{GBi}} \right) = I_{GB} * \vec{\omega_{Bf}} + \left( \vec{r}_{G_B/P} \times m_A \vec{v_{GBf}} \right)\] |
Finally, we can also use the coefficient of restitution equation, at least assuming we know what this coefficient is. For this equation, it will be important to look at the velocities at the point of impact (P) and to specifically look at the velocities normal to the plane of impact, similar to what we did with particles.
| \[e=-\frac{v_{APnf} - v_{BPnf}}{v_{APni} - v_{BPni}}\] |
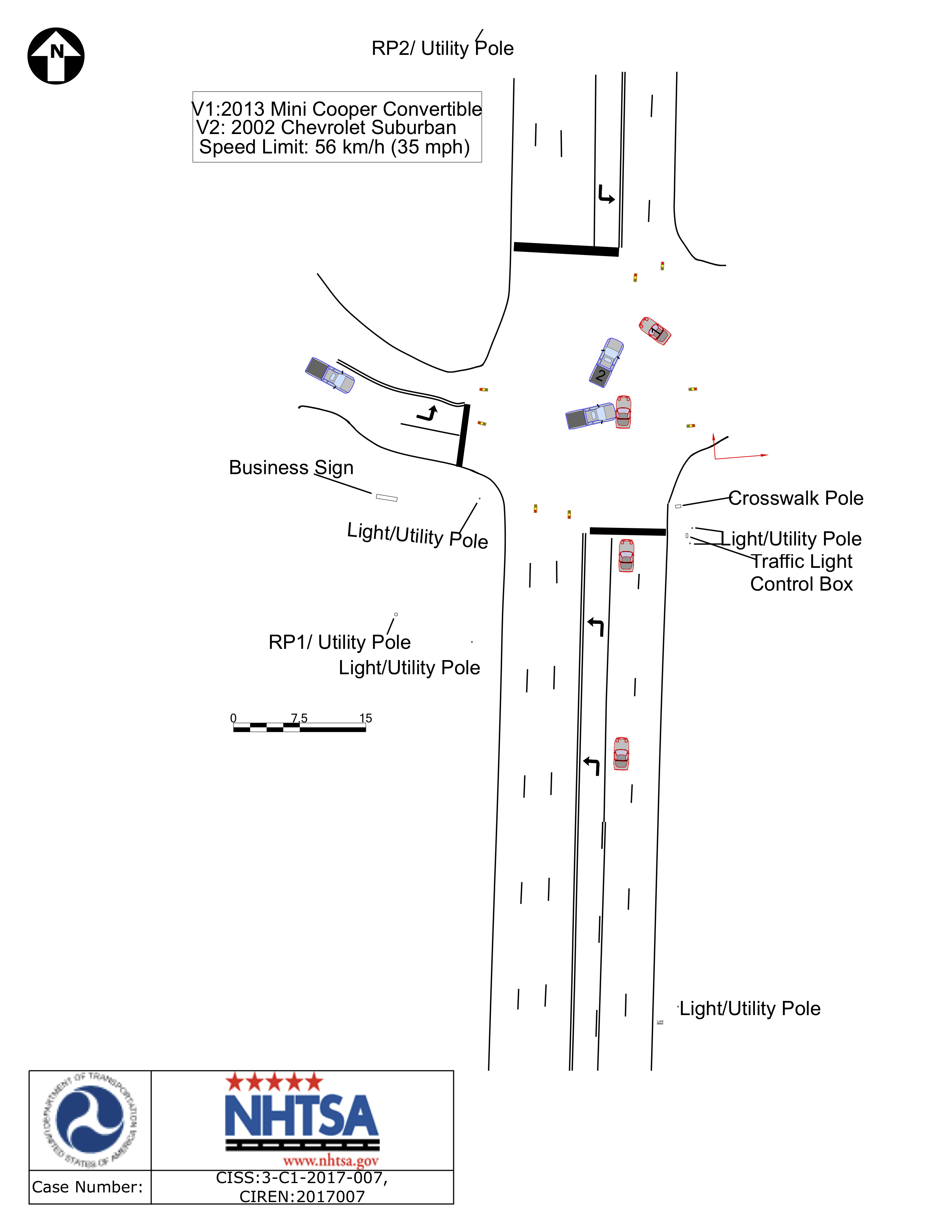
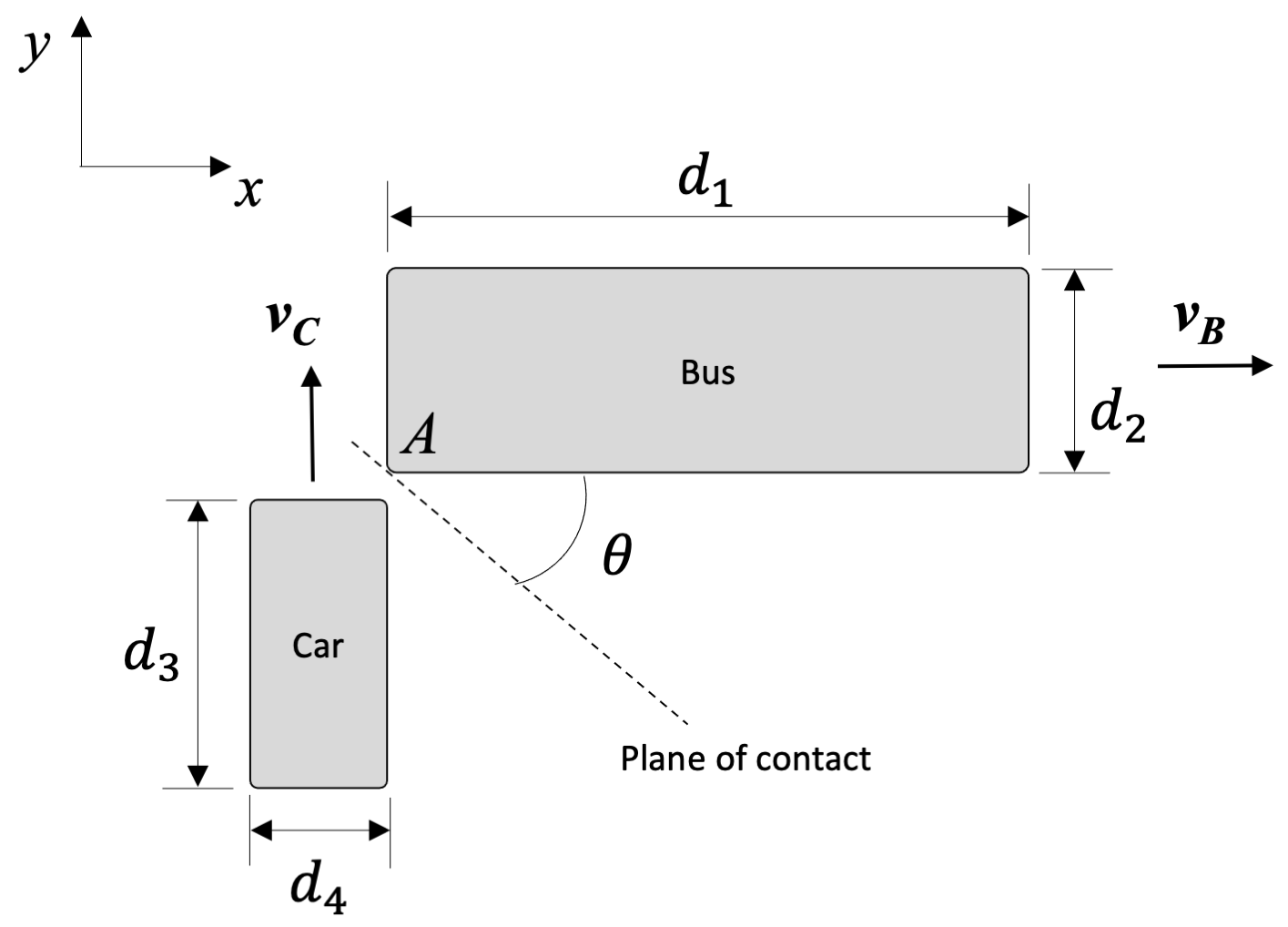
Along with kinematic relationships, combinations of the above equations and strategies can allow us to analyze post-impact motion of the objects. This is useful in areas such as accident reconstruction, where engineers determine what happened in a vehicular crash.