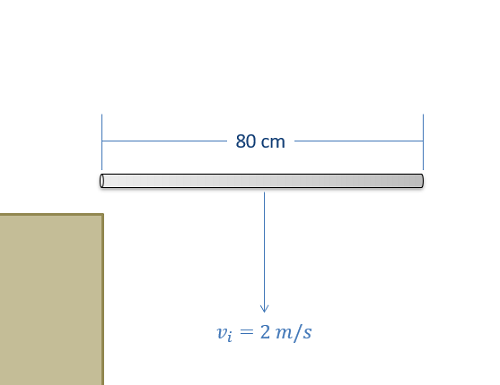
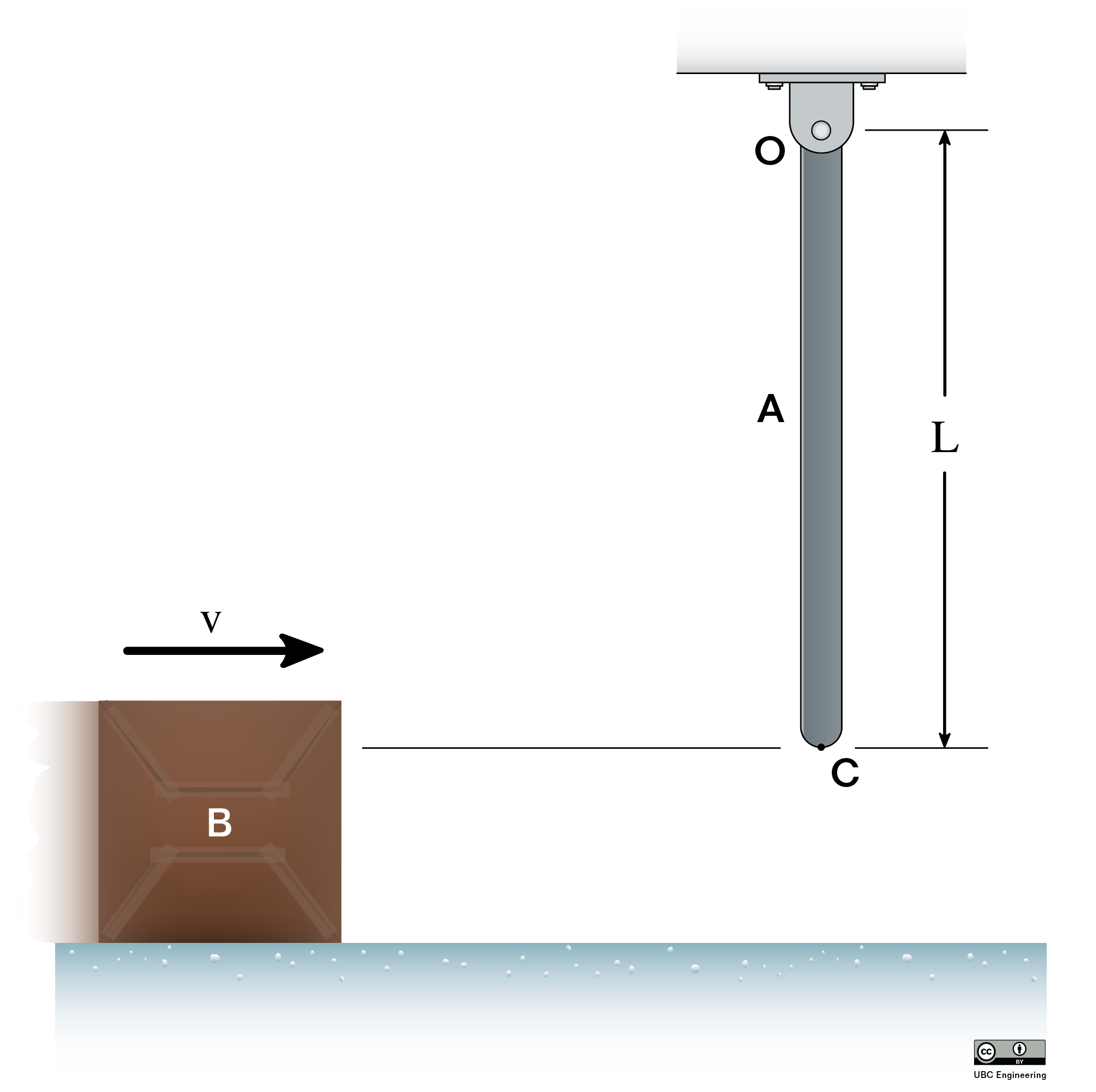
Rigid Body Surface Collisions
In instances where a moving rigid body impacts a solid and immovable surface, the resulting impact can seem chaotic. However, we can still use the ideas of impulse and momentum to predict this impact behavior.
Just as it was with particles, an important first step in solving rigid body impact with a surface problems is to identify the normal and tangential directions. The normal direction will be perpendicular to the surface being impacted while the tangential direction will be parallel to the surface being impacted. Also important for rigid body impact is to identify both the center of mass for the body (G) and the point of impact between the body and the surface (P).
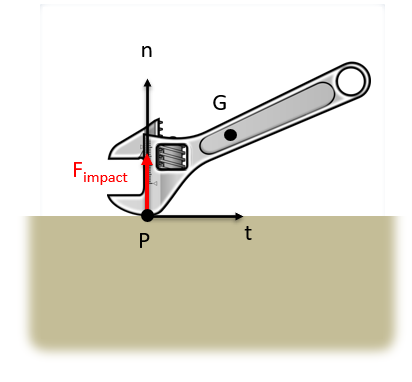
Given we know everything about the motion of a body before the impact, to predict the linear velocity in two dimensions well as the angular velocity after the impact (a total of three unknowns) we will need three equations. These equations will be derived from from the conservation of momentum as well as the application of the coefficient of restitution.
For momentum, we will first notice that the forces during impact will always be in the normal direction. Assuming negligible friction forces (which would be in the tangential direction) we will have no change in linear momentum in the tangential direction and assuming the mass stays constant no change in velocity in the tangential direction at the center of mass of the body.
| \[v_{tGi}= v_{tGf}\] |
Next, examining the coefficient of restitution will give us another equation. Specifically, the coefficient of restitution relates the velocities before and after the collision in the normal direction at the point of impact.
| \[e=-\frac{v_{Pnf}}{v_{Pni}}\] |
Finally, because the force of the impact (and therefore the impulse of the impact) is so large, the forces at any other point will generate negligible impulses in comparison. The impact impulse will primarily determine how the object moves after impact. Therefore about the location of impact, where the impact force does not exert a moment, we can say that angular momentum is conserved. This is the only point about which angular momentum is conserved in an impact.
Since the point of impact is typically not the center of gravity or a pin, we often need to use the general expression of angular momentum.
| \[I_G * \vec{\omega_i}+\left( \vec{r}_{G/P}\times m * \vec{v_Gi} \right) = I_G * \vec{\omega_f}+\left( \vec{r}_{G/P}\times m * \vec{v_Gf} \right)\] |
Between the equations above and whatever relevant kinematics relationships are necessary to relate velocities at the center of mass and the point of impact we should be able to solve for up to three unknowns, allowing us to completely predict the velocities after impact, assuming we know the pre-impact velocities and the coefficient of restitution for the impact itself.