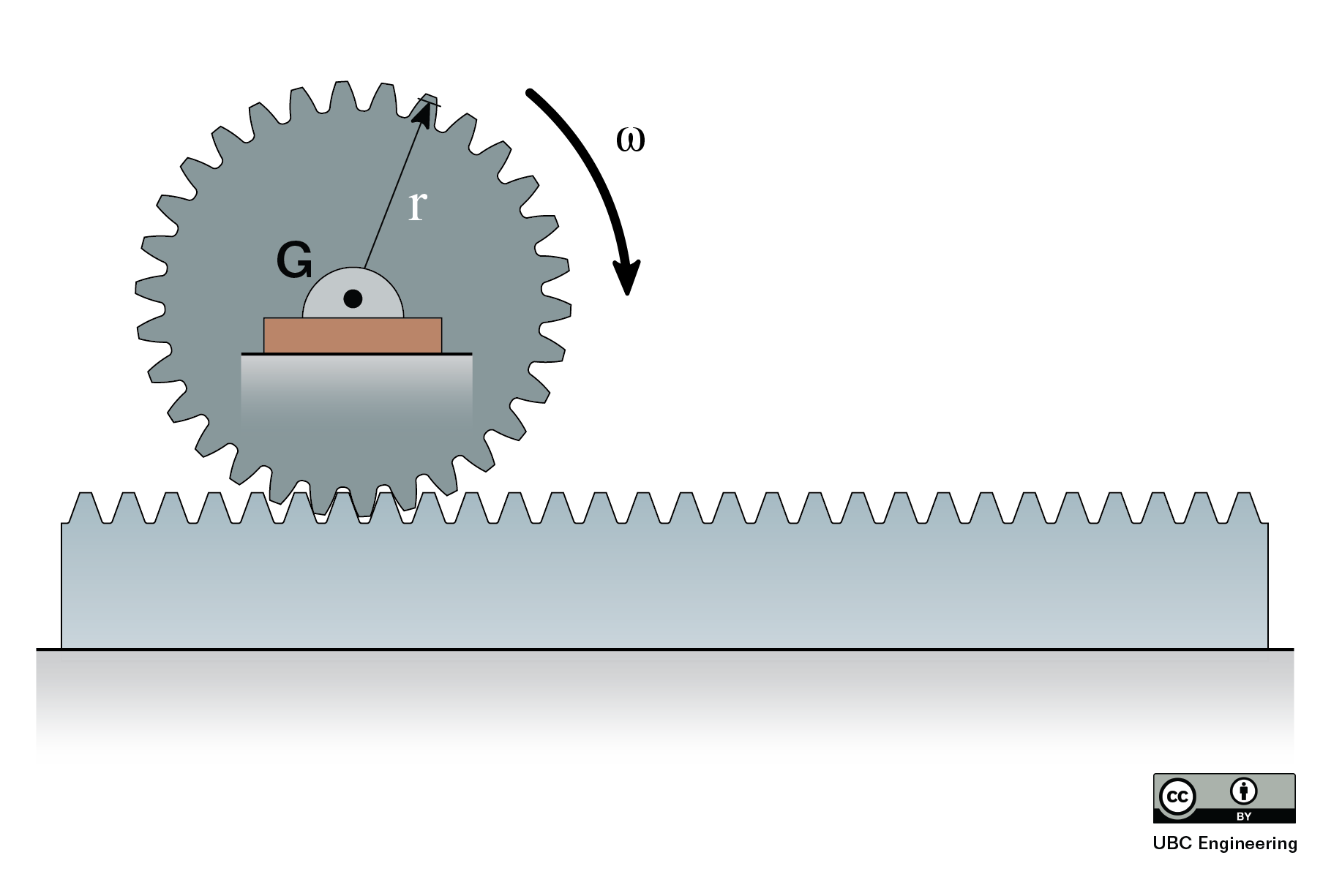
The Impulse Momentum Theorem for a Rigid Body
The Impulse-Momentum Theorem states that the impulse exerted on a body will be equal to the change in momentum of that body. In rigid body systems, this refers to both the linear impulse and momentum as well as the angular impulse and momentum. In equation form, this leads us to out two base equations.
| \[\Delta \vec{J} = m \vec{v_{f}}-m \vec{v_{i}}\] |
| \[\Delta \vec{K} = I \vec{\omega_{f}}-I \vec{\omega_{i}}\] |
A few things to note about the equations above when dealing with impulse momentum problems. First is that the above equations are vector equations, and can be split apart into components. For two dimensional problems, we will commonly break the linear impulse momentum equation into x and y component equations, while the angular impulse momentum equation will be about the z direction. Second, the velocities in the linear impulse momentum equation should always refer to the velocity of the center of mass of the body. And finally, for the angular impulse momentum equation, we can take the impulse and momentum about any point we choose so long as we are consistent within the equation. If the impulse is taken about a certain point then the momentum terms must also be taken about that same point. You can see the previous section for more information on angular momentum about various points.
Solving Impulse Momentum Problems:
With impulse momentum problems, the best place to start is with a diagram. The point of the diagram is to show the initial state, the final state, and the forces and moments in between causing the change. In your diagram you should show any known masses, mass moments of inertia, any known velocities (magnitude and direction), angular velocities, any forces or moments causing an impulse, and the time these forces or moments are exerted for.
After creating a diagram, the next step is to set up your impulse momentum equations. Determine how many equations you are going to use. In 2D problems you have up to three scalar equations, but you may not always need all three equations. You will also need to determine other key factors such as what point you are taking the angular impulse and momentum about. Whatever point you choose, make sure to identify that in your work.
After choosing your equations, plug in any known values for the initial or final states, as well as the impulses acting on the body between these points. At this stage, it is important to remember that moments can come either in the form of a torque directly applied to a body, or as an off-center force causing a linear and angular impulse at the same time.
Finally, the last step is to solve the equations for the unknowns. Make sure you have at least as many equations as unknowns. If you have more unknowns than you can solve for, you may need to use kinematics to relate values such as linear and angular velocity.
Conservation of Angular Momentum:
In instances where there is no external angular impulse on an object, we can see that the angular momentum of the object will remain unchanged. This is known as the conservation of angular momentum, which is simply an extension of the Impulse Momentum Theorem.
| \[\Delta \vec{K} = 0 = I \vec{\omega_{f}}-I \vec{\omega_{i}}\] |
| \[I \vec{\omega_{f}} = I \vec{\omega_{i}}\] |
The conservation of momentum is used primarily in two instances. The first is when spinning bodies change shape. In this case the change in shape of the body will usually increase or decrease the mass moment of inertia of the body about the axis it is spinning about. In order for angular momentum to be conserved, the angular velocity of the body must change such that the angular momentum as a whole remains the same.

The second instance in which the conservation of momentum is applied is in rigid body collisions. In these cases, forces but no moments will be exerted at the point of impact in the collision. This means that a linear impulse is exerted, but no angular impulse is exerted. With no angular impulse about the point of impact, the angular momentum of the bodies must be conserved about that specific point, and this conservation of angular momentum equation will be an important tool in solving rigid body collision problems as discussed in the next few sections.