Work, Kinetic Energy, and Potential Energy for Rigid Bodies
The concepts of Work and Energy provide the basis for solving a variety of kinetics problems. In rigid bodies, as with particles, we will break energy into kinetic energy and potential energy, giving us a base work and energy equation as follows.
| \[W=\Delta KE + \Delta PE\] |
Before jumping into the application of the work and energy equation through, it is important to define all the pieces as they relate to rigid body systems.
Work:
As discussed before, work in general is a force exerted over a distance. In rigid body systems however we will also need to consider work done by moments, where the work of a constant moment is equal to the magnitude of the moment times angular displacement the body moves through (in radians). To find the overall work, we simply need to add the work done by forces and the work done by moments
| \[W=F*d+M*\Delta\theta\] |
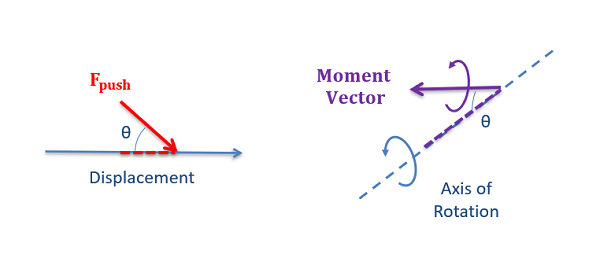
When dealing with the work of forces and the work of moments, it is also important to note the direction of the force and moment vectors. Only the component of the force along the direction of displacement will be included in the work, and similarly only the component of the moment vector along the direction of the axis of rotation will be included in the work. Forces that oppose the displacement, or moments that oppose rotation will be negative work values.
Finally, in cases where the force and/or moment are not constant values, we will need to integrate these values over the distance traveled and the angular displacement respectively.
| \[W=\int_{x1}^{x2} F(x)dx+\int_{\theta1}^{\theta2} M(\theta)d\theta\] |
Kinetic Energy:
Kinetic energy is the energy of mass in motion, and for a rigid body system we will have to worry about both translation and rotation. The translational kinetic energy will be equal to one half of the mass of the body times its velocity (taken at the center of mass) squared, while the rotational kinetic energy will be equal to one half of the mass moment of inertia (also taken about the center of mass) times the angular velocity squared.
| \[KE=\frac{1}{2}mv_G^{2}+\frac{1}{2}I_G\omega^{2}\] |
Alternatively, if we have fixed axis rotation or if we are instead using the instantaneous center of zero velocity, we can take just the rational kinetic energy about that point.
| \[KE=\frac{1}{2}I_O\omega^{2}\] |
| \[KE=\frac{1}{2}I_{IC}\omega^{2}\] |
As a reminder, kinetic energy is a scalar value, having a magnitude but not a direction. The kinetic energy itself cannot be broken into components, and it will always be a positive number since the velocity values are squared.
If we wish to determine the change in kinetic energy, we would simply take the final kinetic energy minus the initial kinetic energy.
| \[\Delta KE=\left (\frac{1}{2}mv_{Gf}^{2}+ \frac{1}{2}I_G\omega_{f}^{2} \right )- \left( \frac{1}{2}mv_{Gi}^{2} + \frac{1}{2}I_G\omega_{i}^{2}\right )\] |
Potential Energy:
Potential energy, unlike kinetic energy, is not really energy at all. Instead, it represents the work that a given conservative force will potentially do between two instants in time. Potential energy can come in many forms, but the two we will discuss here are gravitational potential energy, and elastic potential energy. These represent the work that the gravitational force and a spring force will do, respectively. We often use these potential energy terms in place of the work done by gravity or springs respectively. When including these potential energy terms, it's important to not also include the work done by gravity or spring forces in your equation.
Gravitational Potential Energy
The change in gravitational potential energy for any system is represented by the mass of the body, times the value g (9.81 m/s2 or 32.2 ft/s2 on the earth's surface) times the vertical change in height between the start position and the end position. In equation form, this is as follows.
| \[\Delta PE_{gravity}=m*g*\Delta h\] |
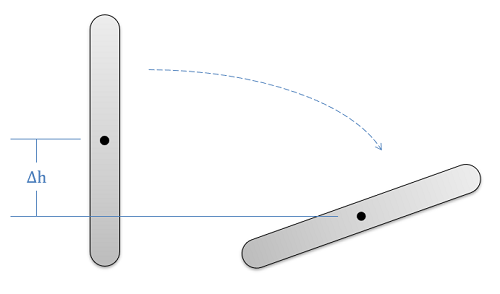
Unlike work and kinetic energy, there is no rotational version of gravitational potential energy, so this is exactly the same as we had for particles. The only important difference we will encounter, is that the change in height will need to specifically be the change in height of the center of mass of the body, not the change in height of some other point.
Elastic Potential Energy
To determine the elastic potential energy in a rigid body system, we will have to take into account any linear springs (as we had for particles) as well as any torsional springs in our system.

To find the elastic potential energy, we will need to know the stiffness of any spring in the problem (represented by k, in units of force per distance for linear springs or moment per angle of twist for torsional springs) as well as the distance or angle the spring has been stretched above or below its natural resting position. This difference from resting position is represented by distance x for linear springs, or angle theta for torsional springs. Once we have those values, the elastic potential energy can be calculated by multiplying one half of the stiffness by the distance x squared or the angle theta squared.
| \[PE_{linear spring}=\frac{1}{2}kx^{2}\] |
| \[PE_{torsional spring}=\frac{1}{2}k\theta^{2}\] |
To find the change in elastic potential energy, we simply take the final elastic potential energy minus the initial elastic potential energy.
| \[\Delta PE_{linear spring}=\frac{1}{2}kx_{f}^{2}-\frac{1}{2}kx_{i}^{2}\] |
| \[\Delta PE_{torsional spring}=\frac{1}{2}k\theta_{f}^{2}-\frac{1}{2}k\theta_{i}^{2}\] |
It's also important to remember that in the equations above, x is not the length of the spring but instead the distance the spring has been stretched or compressed beyond its unstretched length. Similarly theta is not the angle of the torsional spring, but the angle the spring has been twisted away from its resting angle.