Two Dimensional Kinematics in Polar Coordinate Systems
Two Dimensional Motion (also called Planar Motion) is any motion in which the objects being analyzed stay in a single plane. When analyzing such motion, we must first decide the type of coordinate system we wish to use. The most common options in engineering are rectangular coordinate systems, normal-tangential coordinate systems, and polar coordinate systems. Any planar motion can potentially be described with any of the three systems, though each choice has potential advantages and disadvantages.
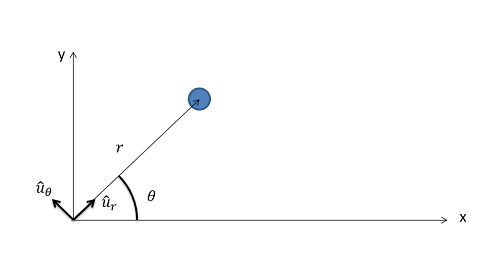
The polar coordinate system uses a distance (r) and an angle (theta) to locate a particle in space. The origin point will be a fixed point in space, but the r-axis of the coordinate system will rotate so that it is always pointed towards the body in the system. The variable "r" is also used to indicate the distance from the origin point to the particle. The theta axis will then be 90 degrees counter clockwise from the r-axis with the variable "theta" being used to show the angle between the r-axis and some fixed axis that does not rotate.. The diagram below shows a particle with a polar coordinate system.
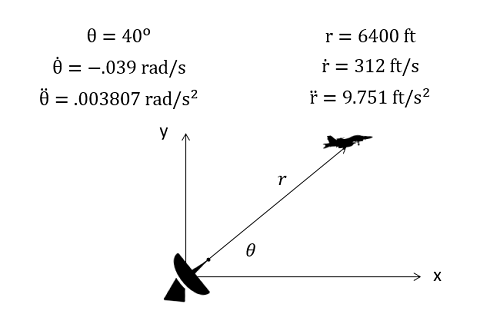
Polar coordinate systems work best in systems where a body is being tracked via a distance and an angle such as a radar system tracking a plane. In cases such as this, the raw data from this in the form of an angle and a distance would be direct measures of theta and r respectively. Polar coordinate systems will also serve as the base for extended body motion, where motors and actuators can directly control things like r and theta.
The way the coordinate system is defined, the r-axis will always point from the origin point to the body. The distance from the origin to the point is defined as "r" with no component of the position being in the theta direction.
| Position: | \[r_{p/o}(t)=r\hat{u}_{r}+0\hat{u}_{\Theta}\] |
|---|
To find the velocity, we need to take the derivative of the position function over time. Since the distance r can change over time as well as the direction r changing over time to track the body, we need to worry about the derivative of r as well as the derivative of the unit vector. Like we did with the normal-tangential systems, we will use the product rule and then substitute in a value for the derivative of the unit vector.
| Velocity: | \[v(t)=\dot{r}\hat{u}_{r}+r\dot{\hat{u}_{r}}=\dot{r}\hat{u}_{r}+r\dot{\Theta}\hat{u}_{\Theta}\] |
|---|
To find the acceleration, we need to take the derivative of the velocity function. As all of these terms, including the unit vectors, change over time, we will need to use the product rule extensively. The u-r term will split into two terms, and the u-theta term will split into three terms.
| Acceleration: | \[a(t)=\ddot{r}\hat{u}_{r}+\dot{r}\dot{\hat{u}_{r}}+\dot{r}\dot{\Theta}\hat{u}_{\Theta}+r\ddot{\Theta}\hat{u}_{\Theta}+r\dot{\Theta}\dot{\hat{u}_{\Theta}}\] |
|---|
Again we will need to substitute in values for the derivatives of the unit vectors similar to before, but it is worth mentioning that the derivative of the u-theta vector as it rotates counter clockwise is in the negative u-r direction.
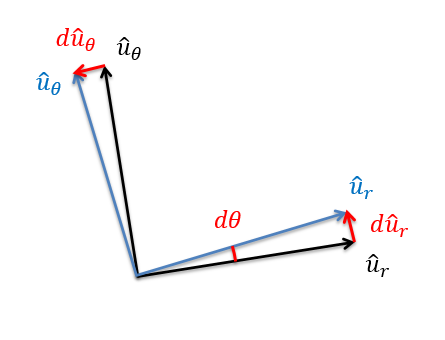
After substituting in the derivatives of the unit vectors and simplifying the function we arrive at our final equation for the acceleration.
| Acceleration: | \[a(t)=\ddot{r}\hat{u}_{r}+\dot{r}\dot{\Theta}\hat{u}_{\Theta}+\dot{r}\dot{\Theta}\hat{u}_{\Theta}+r\ddot{\Theta}\hat{u}_{\Theta}-r\dot{\Theta}^{2}\hat{u}_{r}\] |
|---|---|
| \[=(\ddot{r}-r\dot{\Theta}^{2})\hat{u}_{r}+(2\dot{r}\dot{\Theta}+r\ddot{\Theta})\hat{u}_{\Theta}\] |
Though this final equation has a number of terms, it is still just two components in vector form. Just as with the normal-tangential coordinate system, we will need to remember that we will need to split the single vector equation into two separate scalar equations. In this case we will have the equation for the terms in the r direction and the equation for the terms in the theta direction.