The Work and Energy Principle for a Particle
As stated in the previous section, the Principle of Work and Energy can be boiled down to the idea that the work done to a body will be equal to the change in energy of that body. Dividing energy into kinetic and potential energy pieces as we often do in dynamics problems, we arrive at the following base equation for the conservation of energy.
| \[W=\Delta KE + \Delta PE\] |
In the equation above, it is important to notice that unlike Newton's Second Law, the work and energy equations are not vector equations. They do not need to be broken down into components which will simplify the math, however, with only single equation we can only solve for a single unknown. This tends to be the limiting factor when using work and energy methods.
Solving Work and Energy Problems
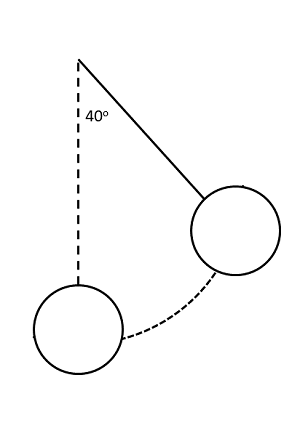
To solve work and energy problems, we will need to first clearly define the initial state and the final state. Drawing a diagram that clearly shows each of these can be a useful first step. These are not free body diagrams as we used in the last chapter, but they do serve the same purpose in that they are a step towards setting up our equations.
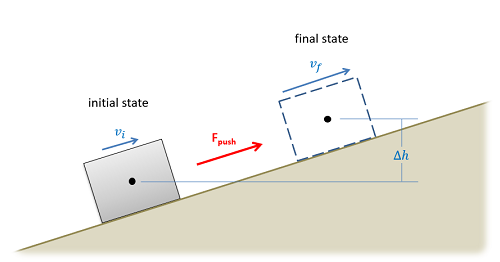
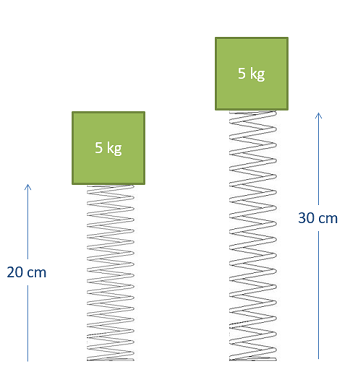
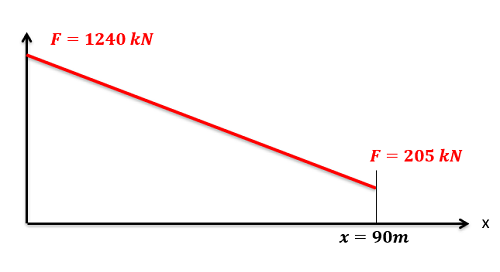
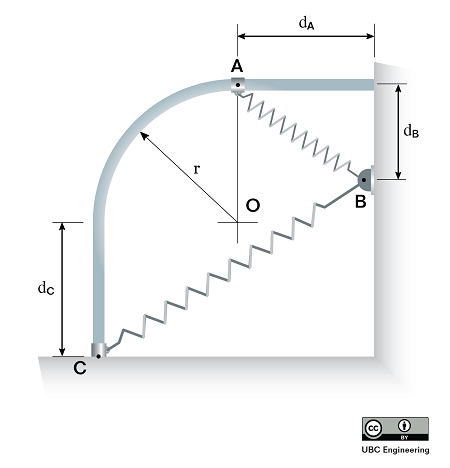
After clearly defining the initial and final states, we will start plugging values into our work and energy equation. Add a work term for any external force acting on the system between the initial and final states (excluding gravity forces and spring forces). Determine the kinetic energy in the initial state and the final state and plug those into the equation, if there is a change in height plug in change in gravitational potential energy terms, and if there are any springs plug in any elastic potential energy terms.
After plugging in all the terms, you should hopefully have only a single unknown value that you can solve for. If you have more than one unknown, you may need to use geometry, kinematics, or dependent motion analysis to relate the unknowns that you do have.
After putting all the terms into the work and energy equation and ensuring that there is only a single unknown, you will simply need to use algebra to solve for the unknown in the equation.
The Conservation of Energy
In the subset of work and energy problems where there is no external work done to the body (again excluding gravity and springs), we can eliminate this term from the equation. Instances such as this are known as conservation of energy problems, since the initial and final energies as a whole must be equal to one another.
| \[KE_i + PE_i =KE_f + PE_f\] |
Conservation of energy problems are solved in the same manner as other work and every problems, by setting up a diagram, plugging values into your equation, and solving for the unknown. The only difference is that we need to be sure that there are no external forces doing work on the body, and that we use a different base equation.