Moment Integrals
A moment integral, as the name implies, is the general concept using integration to determine the net moment of a force that is spread over an area or volume. Because moments are generally a force times a distance, and because distributed forces are spread out over a range of distances, we will need to use calculus to to determine the net moment exerted by a distributed force.
| \[\int M=\int F(d)*d\] |
Beyond the most literal definition of a moment integral, the term 'moment integral' is also applied the general process of integrating distributed areas or masses that will be resiting some moment about a set axis.
Some of the applications of moment integrals include:
- Finding point loads that are equivalent to distributed loads (the equivalent point load)
- Finding the centroid (geometric center) or center of mass for 2D and 3D shapes.
- Finding the area moment of inertia for a beam cross section, which will be one factor in that beam's resistance to bending.
- Finding the polar area moment of inertia for a shaft cross section, which will be one factor in that shaft's resistance to torsion.
- Finding the mass moment of inertia, indicating a body's resistance to angular accelerations.
When looking at moment integrals, there are number of different types of moment integrals. These will include moment integrals in one dimension, two dimensions, and three dimensions, moment integrals of force functions, of areas/volumes, or of mass distributions, first order or second order moment integrals, and rectangular or polar moment integrals.
Any combination of these different types is possible (for example a first, rectangular, 2D, area moment integral or a second, polar, 3D, mass moment integral). However, only some combinations will have practical applications and will be discussed in detail on future pages.
1D, 2D, and 3D Moment Integrals
Technically we can take the moment integral in any number of dimensions, but for practical purposes we will never deal with moment integrals beyond 3 dimensions. The number of dimensions will affect the complexity of the calculations (with 3D Moment integrals being the more involved than 1D or 2D moment integrals), but the nature of the problem will dictate the dimensions needed. Often this is not listed in the type of moment integral, requiring you to assume the type based on the context of the problem.
Force, Area/Volume, and Mass Moments Integrals
The next distinction in moment integrals is regard what we are integrating. Generally, we can integrate force functions over some distance, area, or volume, we can integrate the area or volume function itself, or we can integrate the mass distribution over the area or volume. Each of these types of moment integrals has a different purpose and will start with a different mathematical function to integrate, but the integration process beyond that will be very similar.
First vs. Second Moments Integrals
For moment integrals we will always be multiplying the force function, area or volume function, of the mass distribution function by a distance, or a distance squared. First moment integrals just multiply the initial function by the distance, while second moment integrals multiply the function by the distance squared. Again the type of moment integral we will use depends upon our application, with things like equivalent point load, centroids, and center of mass relying on first moment integrals, and area moments of inertia, polar moments of inertia, and mass moments of inertia relying on second moment integrals. As you can probably deduce from this list, second moment integrals, are often labeled as a 'moment of inertia'
Rectangular vs. Polar Moments Integrals
Finally we will talk about rectangular moments integrals versus polar moments integrals. This is a difference in how we define the distance in our moment integral. Let's start with the distinction in 2D. If our distance is measured from some axis (for example the x-axis, or the y-axis) then it is a rectangular moment integral. If on the other hand the distance is measured from some point (such as the origin) then it is a polar moment integral.
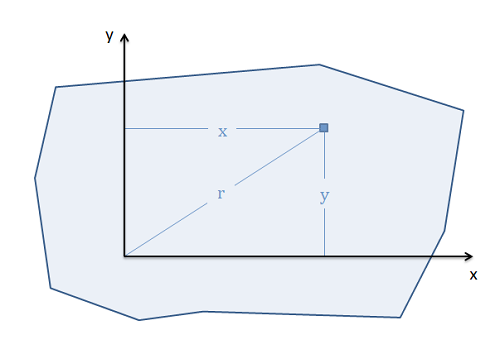
This distinction is important for how we will take the integral. For rectangular moment integrals we will move left to right or bottom to top. For polar moment integrals we will instead take the integral by radiating out from the center point.
In three dimensional problems, the definitions change slightly. For rectangular moment integrals the distance will be measured from some plane (such as the xy plane, xz plane, or yz plane). Again we will integrate left to right, bottom to top, or now back to front with distances corresponding to the x, y or z coordinates of that point. For a polar moment integrals the distance will be measured from some axis (such as the the x, y, or z axis), and we will integrate by radiating outward from that axis.