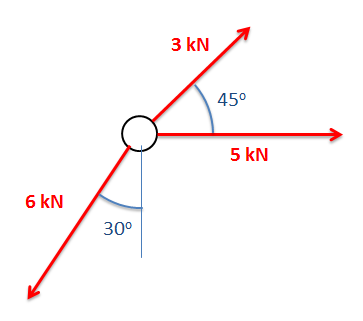
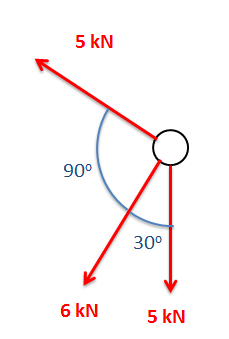
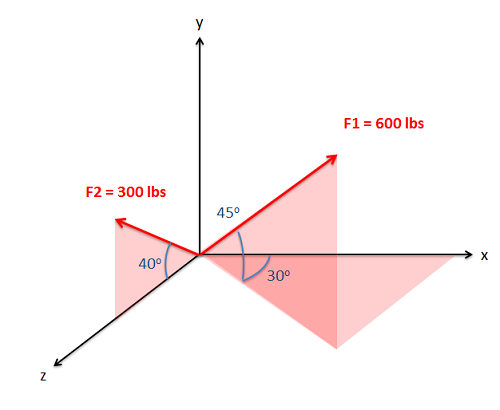
Vector Addition
The most common thing we will need to do with many vector quantities is to add them up. The sum of these vector quantities is the net vector quantity. For example, if we have a number of forces acting on a body, the sum of those forces is known as the net force.
The sum of any number of vectors can be determined geometrically using the following strategy. Starting with one of the vectors as the base, we redraw the second vector so that the tail of the second vector begins at the tip of the first vector. We can repeat this with a third vector, a fourth vector and so on, putting the tail of each vector at the tip of the last vector until we have taken all vectors into account. Once the vectors are all drawn tip to tail, the sum of all the vectors will be the vector connecting the tail of the first vector to the tip of the last vector.
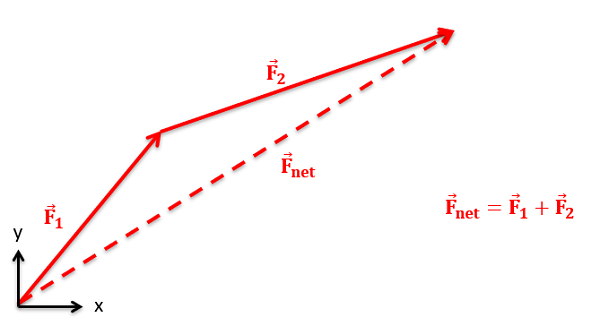
In practice, The easiest way to determine the magnitude and direction of the sum of the vectors is to add the vectors in component form. This starts by separating each vector into x, y, and possibly z components. As we can see in the diagram below, the x component of the sum of all the vectors will be the sum of all the x components of the individual vectors. Similarly the y and z components of the sum of the vectors will be the sum of all the y components and the sum of all the z components respectively.
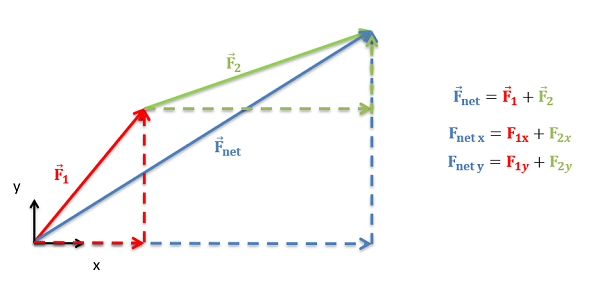
Once we find the sum of the components in each direction, we can either leave the net vector in component form, or we can use the Pythagorean theorem and inverse tangent functions to convert the vector back into a magnitude and direction as detailed on the "vectors" page.