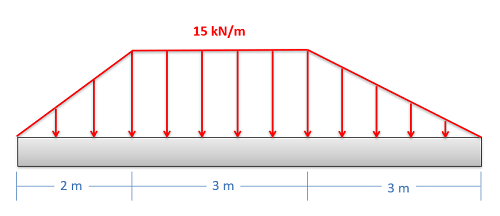
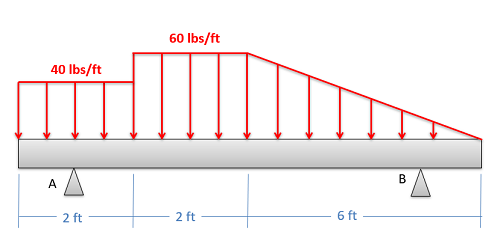
Equivalent Point Load (via Composite Parts)
As stated previously, an equivalent point load is a single point force that will have the same effect on a body as the original loading condition, which is usually a distributed force.
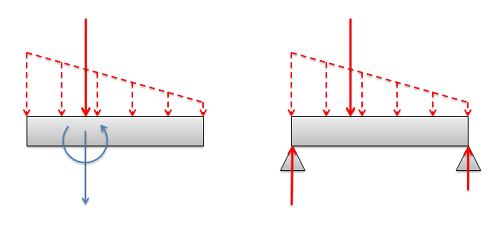
Finding the Equivalent Point Load
When finding the equivalent point load we need to find the magnitude, direction, and point of application of a single force that is equivalent to the distributed force we are given. In this course we will only deal with distributed forces with a uniform direction, in which case the direction of the equivalent point load will match the uniform direction of the distributed force. This leaves the magnitude and the point of application to be found. There are two options available to find these values:
- We can find the magnitude and the point of application of the equivalent point load via integration of the force functions.
- We can use the area/volume and the centroid of the area or volume under the force function.
The first method is more flexible, allowing us to find the equivalent point load for any force function that we can make a mathematical formula for (assuming we have the skill in calculus to integrate that function). The second method is usually faster, assuming that we can look up the values for the area or volume under the force curve and the values for the centroid of the area or volume under the force function. On this page we will be focusing on the second method.
Using the Area and Centroid for Distributed Forces in Beams:
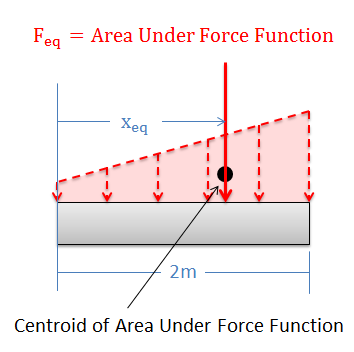
As an alternative to using integration, we can use the area under the force curve and the centroid of the area under the force curve to find the equivalent point load's magnitude and point of application respectively.
The magnitude (Feq) of the equivalent point load will be equal to the area under the force function. We can find this area using calculus, but there are often easier geometry based ways of finding the area under the force function. If that is an option, you can always use geometry to find the area under the force function curve which is equal to the magnitude of your equivalent point load. Note that the width of this area will be in units of distance, while the height of this area will be in units of force per unit of distance. This means that the resulting area will be in units of force.
The equivalent point load will also always travel through centroid of the area under the force function. On the previous page we used the moment integral to find this location, but we can alternatively use the method of composite parts to identify the centroid. For more information on using the method of composite parts to identify the centroid of an area, refer to Appendix 2.
Using Volumes and Centroids in Surface Force Problems:
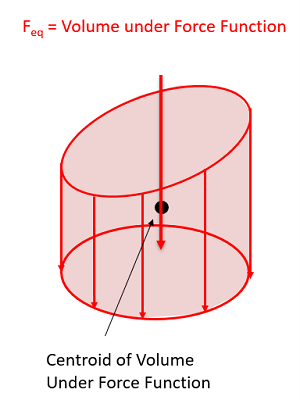
Just as in the 2D problems, there are some available shortcuts to finding the equivalent point load in 3D surface force problems. For a force spread over an area, the magnitude (Feq) of the equivalent point load will be equal to the volume under the force function. Rather than integrating, if there is a geometry based way of finding the volume, you can use that instead of integration.
Additionally, the equivalent point load will also always travel through the centroid of the volume under the force function. For simple shapes you may be able to identify this centroid directly from the 3D Centroids table. For more complex setups, you may need to employ the method of composite parts to find the overall centroid. For more information on finding centroids via composite parts see Appendix 2.