Distributed Forces

A distributed force is any force where the point of application of the force is an area or a volume. This means that the "point of application" is not really a point at all. Though distributed forces are more difficult to analyze than point forces, distributed forces are quite common in real world systems so it is important to understand how to model them.

Distributed forces can be broken down into surface forces and body forces. Surface forces are distributed forces where the point of application is an area (a surface on the body). Body forces are forces where the point of application is a volume (the force is exerted on all molecules throughout the body). Below are some examples of surface and body forces.

The Hoover Dam
The water pressure pushing on the surface of this dam is an example of a surface force. Image by Curimedia CC-BY-SA 2.0
Airplane
The gravitational force on this apple is distributed over the entire volume of the fruit. Gravitational forces are an example of body forces. Image by Zátonyi Sándor CC-BY 3.0

Representing Distributed Forces:

Distributed forces are represented as a field of vectors. This is drawn as a number of discrete vectors along a line, over a surface, or over a volume, that are connected with a line or a surface as shown below.

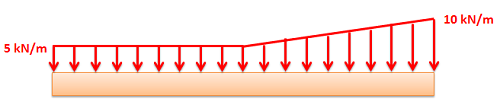
Force Distributed over a Line
This is a representation of a surface force in a 2D problem (A force distributed over a line). The magnitude is given in units of force per unit distance.
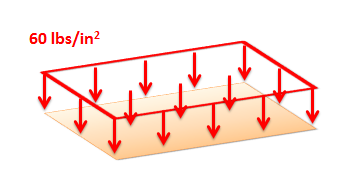
Force Distributed over a surface
This is a representation of a surface force in a 3D problem (a force distributed over an area). The magnitude is given in units of force per unit area (also called a pressure).

Though these representations show a discrete number of individual vectors, there is actually a magnitude and direction at all points along the line, surface, or body. The individual vectors represent a sampling of these magnitudes and directions.

It is also important to realize that the magnitudes of distributed forces are given in force per unit distance, area, or volume. We must integrate the distributed force over its entire range to convert the force into the usual units of force.

Analyzing Distributed Forces:

For analysis purposes in statics and dynamics, we will usually substitute in a single point force that is statically equivalent to the distributed force in the problem. This single point force is called the equivalent point load and it will cause the same accelerations or reaction forces as the distributed force while simplifying the math. In the strength of materials context where the bodies are not rigid, this substitution will not work however as the distributed forces will not cause the same deformations and stresses as the point force.