Orientation, Angular Displacement, Angular Velocity, and Angular Acceleration
When discussing rigid bodies that can both translate and rotate, we will need to discuss the concepts of orientation, angular displacement, angular velocity, and angular acceleration, in addition to position, displacement, velocity, and acceleration in order to fully describe the motion.
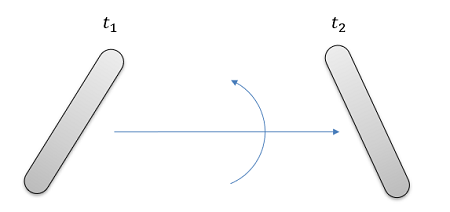
Orientation
The concept of orientation describes how a body is currently rotated relative to a set neutral orientation. Along with the position, it is necessary to fully define the location of a rigid body.
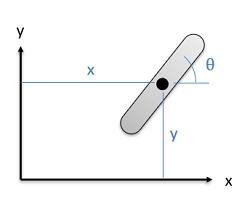
In two dimensional systems, a single angle is enough to fully define the orientation. However, in three dimensional systems a set of three angles is necessary to fully define the orientation. These three angles are usually given as rotations about each of the three coordinate axes.
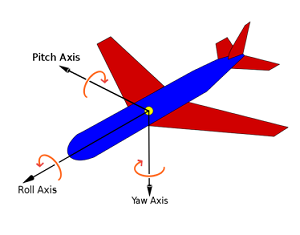
Angular Displacement
The angular displacement is simply the change in orientation between two points in time. In two dimensional systems we can treat this as more or less a scalar quantity (just the rotation clockwise or counterclockwise) but in three dimensional systems, we will need to treat the value as a vector quantity, describing the angle of rotation as well as the axis we are rotating the body about.
Angular Velocity
The angular velocity of a rigid body is defined as the rate of change of orientation over the rate of change of time.
| \[\vec{\omega}=\frac{d\vec{\theta}}{dt}\] |
This is a vector quantity, indicating both a magnitude and a direction for the rotation. The angular velocity vector will line up with the axis of rotation, using the right hand rule to determine the direction of the vector along that axis.

If we are interested in the average angular velocity over some set time period, we would take the change in orientation (which is the angular displacement) over the change in time.
| \[\vec{\omega}_{ave}=\frac{\Delta \vec{\theta}}{\Delta t}=\frac{angular\,displacement}{time}\] |
Angular Acceleration
Finally, the angular acceleration is defined as the rate of change of the angular velocity over time. Since the angular velocity itself is the rate of change of the orientation over time, the angular acceleration is the double derivative of the orientation with respect to time.
| \[\vec{\alpha}=\frac{d\vec{\omega}}{dt}=\frac{d^2\vec{\theta}}{dt^2}\] |
As with angular displacement and angular velocity, acceleration is a vector quantity with both a magnitude and direction. Just as with angular velocity, we can use the right hand rule to determine the direction of the angular acceleration vector.