Fixed Axis Rotation in Rigid Bodies
When moving from particle kinematics to rigid body kinematics, we add the rotation of a body into the motion analysis process. Some bodies will translate and rotate at the same time, but many engineered systems have components that simply rotate about some fixed axis. We will start our examination of rigid body kinematics by examining these fixed axis rotation problems, where rotation is the only motion we need to worry about.

|
|
Angular Position, Velocity, and Acceleration.
Just as with translational motion, we will have angular positions, which we can take the derivative of to find angular velocities, which we can again take the derivative of to find angular accelerations. Since we can only have a single axis of rotation in two dimensional problems (rotating about the z axis, with counter-clockwise rotations being positive, and clockwise rotations being negative) the equations will mirror the one dimensional equations used in particle kinematics.
| Angular Position: | \[\theta(t)\] |
|---|---|
| Angular Velocity: | \[\omega(t)=\frac{d\theta}{dt}=\dot{\theta}\] |
| Angular Acceleration: | \[\alpha(t)=\frac{d\omega}{dt}=\frac{d^2\theta}{dt^2}=\ddot{\theta}\] |
Also as with one dimensional translational motion, we can use integration to move in the opposite direction (just remember your constants of integration).
| Acceleration: | \[\alpha(t)\] |
|---|---|
| Velocity: | \[\omega(t)=\int \alpha(t)\] |
| Position: | \[\theta(t)=\int \omega(t)=\iint \alpha(t)\] |
If we have constant angular accelerations, we can also use the following formulas adapted from one dimensional motion.
| Acceleration: | \[\alpha(t)=\alpha\] |
|---|---|
| Velocity: | \[\omega(t)=\alpha t+\omega_{0}\] |
| Position: | \[\theta(t)=\frac{1}{2}\alpha t^{2}+\omega_{0}t+\theta_{0}\] |
| Without Time: | \[\omega^{2}-\omega{_{0}}^{2}=2\alpha(\theta-\theta_{0})\] |
Velocity and Acceleration of a Point on a Rotating Body:
With fixed axis rotation, there is a single point on a body that does not move, however all other points on this body will have some velocity and some acceleration due to the rotation of the body itself.
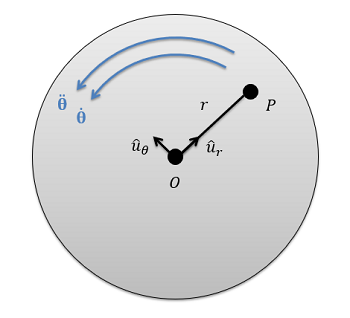
To determine the velocities and accelerations of these points, we will adapt the equations we used for polar coordinates. As a reminder, these equations were as follows:
| Velocity: | \[v=\dot{r}\hat{u}_{r}+r\dot{\Theta}\hat{u}_{\Theta}\] |
|---|---|
| Acceleration: | \[a=(\ddot{r}-r\dot{\Theta}^{2})\hat{u}_{r}+(2\dot{r}\dot{\Theta}+r\ddot{\Theta})\hat{u}_{\Theta}\] |
To simplify the above equations, we can note that for a rigid body, the point P never gets any closer or further away from the fixed center point O. This means that the distance r never changes and the r dot and r double dot terms in the above equations are zero. Putting this to work, we can simplify the above equations into the equations below.
| Velocity: | \[v=r\dot{\Theta}\hat{u}_{\Theta}\] |
|---|---|
| Acceleration: | \[a=(-r\dot{\Theta}^{2})\hat{u}_{r}+(r\ddot{\Theta})\hat{u}_{\Theta}\] |
These equations allow us to find the velocity and acceleration of any point on a body rotating about a fixed axis, given that we know the angular velocity of the body (Theta Dot), the angular acceleration of the body (Theta Double Dot), and the distance from the point to the axis of rotation (r).

