Surface Collisions and the Coefficient of Restitution
Here we will use the term surface collision to describe any instance where a body impacts and rebounds off a solid and unmoving surface. A clear example of a surface collision is a basketball bouncing off a hard floor. The basketball will have some velocity before the collision and some second velocity after the collision, with the floor exerting an impulsive force during the collision that causes this change in velocity.
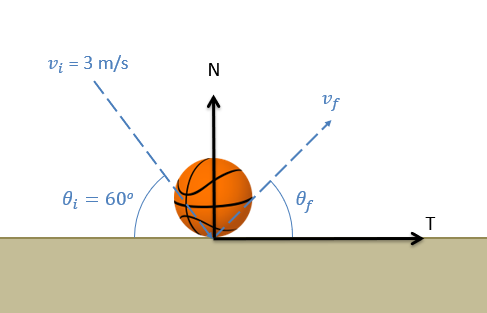
To analyze this collision, we will first need to set up a normal direction (perpendicular to the surface) and a tangential direction (parallel to the surface) for our problem, and break our velocities down into components in these directions. Assuming minimal friction during the impact, we will have an impulsive impact force acting entirely in the normal direction. This fact will form the basis for our analysis.
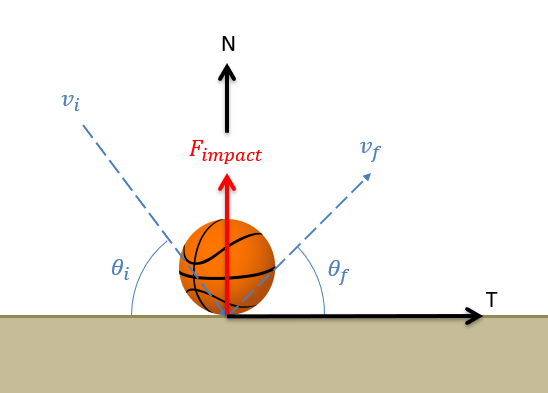
Because the impact force acts entirely in the normal direction, there will be no other significant force to change the momentum of the body in the tangential direction. Assuming the mass remains constant for the body, this means that the velocity must remain constant in the tangential direction because of the conservation of momentum.
| \[v_{it}=v_{ft}\] |
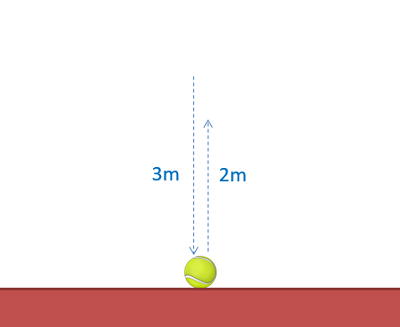
To relate the velocities in the normal direction before and after the collision, we will use something called the coefficient of restitution. The coefficient of restitution is a number between 0 and 1 that measures the "bounciness" of the body and the surface in the collision. Specifically, for a single body being bounced perpendicular off of a surface, the coefficient of restitution is defined as the speed of the body immediately after bouncing off a surface divided by the speed immediately before bouncing off the surface. If we use velocities in place of speed, we will put a negative sign in our equation because the bounce causes a change in direction for the body.
| \[e=-\frac{v_{f}}{v_{i}}\] |
In instances where the body is being bounced off the surface at an angle, the impact force is entirely in the normal direction and the coefficient of restitution relationship specifically applies to the components of the velocities in the normal direction.
| \[e=-\frac{v_{nf}}{v_{ni}}\] |
This relationship can be applied to elastic collisions (where e would be equal to 1), semi-elastic collisions (where e would be some number between 0 and 1) and in-elastic collisions (where e would be equal to 0).