The Work and Energy Principle for Systems of Particles
Just as we used the energy method for a single particle, we can also use the energy method for a system of particles. As a reminder, the conservation of energy equation states that the change in energy of a body (including kinetic and potential energies) will be equal to the work done to a body between during that time.
| \[W=\Delta KE + \Delta PE\] |
For a system of particles, the sum of the work done to all particles will be equal to the change in energy of all particles collectively, essentially combining multiple work and energy equations into one.
| \[\sum W=\sum \Delta KE + \sum \Delta PE\] |
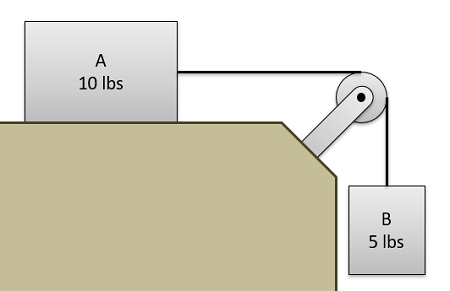
This would seem to make one complex equation out of multiple simple equations (applying the work and energy equation separately to each body), but there is an advantage in that internal forces in the system will cancel out. In the diagram below, we can see a system of two particles connected via a cable. Examining the bodies separately, we would have two tension forces and a friction force all doing work to one box or the other. In the single equation for the system of boxes however, the work down by the two tension forces (one positive and one negative) will sum up to zero. This will be true for any forces that are exerted between the bodies in the system, and forces like these are known as internal forces. The friction force on the other hand is an example of an external force, in that it exists between the top box and the surface (which is not part of our system.
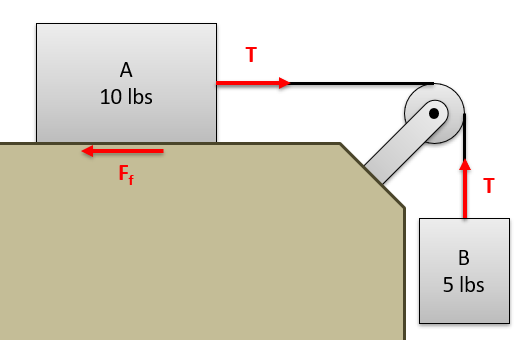
In the end, the sum of work done by external forces will be equal to the change in total energy for the system of particles. Since we only have a single equation, we can only solve for a single unknown. We will often have to go back to our kinematics to relate the velocities and displacements of the various bodies to one another. Since these systems often consist of bodies connected to one another via cables, dependent motion analysis in particular will often come into play.